最近刚看完一个还不错的基于B+ Tree实现的kv引擎,借着这股劲儿刚好补充了一下相关理论知识,对比着看其他资料(资料1、资料2、资料3、资料4)看了下《A Comparison of Fractal Trees to Log-Structured Merge (LSM) Trees》论文,我比较愿意扣细节,所以看得那叫一个费劲,不过里面的分析还挺有意思,所以这里写篇博客,套着论文的结论,按着自己的理解总结一下
相关定义
1. RAM、DAM
RAM(Random Access Machine model)假设计算机有无穷大小的内存,并且访问内存任何地址都用相同的单位时间。当机器实际内存满足某个算法理论需要的内存时,RAM可以很好的描述该算法的复杂度。然而假设机器实际内存不够时,操作系统将部分内存换出到磁盘并在需要时重新换回内存,虽然这对程序自身来说可以无感知,不过客观来看,还是不得不面对此刻的两种“内存”(内存+磁盘),他们的访问时间是100ns和10ms的区别,如此大的差距如果继续使用RAM一视同仁,那么此时对复杂度的分析是不准确的。
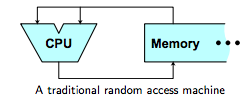
DAM(Disk-Access model也叫Standard External-Memory model)有如下定义:
1. 一台机器有一个处理器、一个可以包含M个objects的内存以及无穷大小的外存
2. 在一次I/O操作中,计算机可以在内存和外存之间传输包含B objects的block,其中1 < B < M
3. 一个算法的Running Time可以定义为在算法执行期间I/O的次数、只用内存数据进行的计算可以认为是没有代价的
4. 一个数据结构的大小可以定义成可以包含它的blocks数的大小
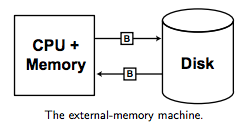
对于外存结构来说,无疑使用DAM来分析不同数据结构的优劣更为合适,只需要分析每种数据结构在各种操作中所涉及的I/O次数即可
2. 读放大、写放大
写放大:Write amplification is the amount of data written to storage compared to the amount of data that the application wrote,也就是说实际写入磁盘的数据大小和程序要求写入数据大小之比
读放大:Read amplification is the number of I/O’s required to satisfy a particular query,也就是一次查询所需要的I/O数
分析
1. B+ Tree
为了方便分析,我们进行相关约定,B+ Tree的block size为B,故每个内部节点包含O(B)个子节点,叶子节点包含O(B)条数据,假设数据集大小为N,则B+ Tree的高度为O((log N/B)/(log B))
写放大:B+ Tree的每次insert都会在叶子节点写入数据,不论数据实际大小,每次都需要写入B,所以写放大是B
读放大:B+ Tree的一次查询需要从根节点一路查到具体的某个叶子节点,所以需要等于层数大小的I/O,也就是O((log N/B)/(log B)), 即写放大为O((log N/B)/(log B))
2. Factal Tree Index
与B+ Tree稍有不同,FTI将每个block从中分一部分用作buffer,假设每个block size 为B,现在每个内部节点拥有K个子节点(k可以等于根号下B),则FTI的高度为O((log N/B)/(log K))
写放大:当root的buffer满了之后,需要将buffer中的records推到子节点的buffer中,一般情况下,每个子节点收到B/K个records,也就是说每B/K个records产生一次I/O,也就是写入B,那么每一个record产生K/B次I/O,也就是写入K,同样一条record,每往下推一层就产生K/B次I/O,写入K,所以一共写入O(K(log N/B)/(log K)),即写放大为O(K(log N/B)/(log K))
读放大:同B+ Tree一样,和树的高度相关,不过此时的高度为O((log N/B)/(log K)),即读放大为O((log N/B)/(log K))
3. LSM Tree
Leveld LSM Tree
假设数据集大小为N,放大因子为k,最小层一个文件大小为B,每层文件的单个文件大小相同都为B,不过每层文件个数不同
写放大:同一个record,会在本层写k次之后才会被compact到下一层,也就是说每次层会放大k,一共有层数O((log N/B)/(log B)),故写放大为O(k(log N/B)/(log B))
读放大:依次在每一层进行二分查找,直到在最后一层找到,即: R = (log N/B) + (log N/Bk) + (log N/Bkk) + … + 1 = (log N/B) + (log N/B) - (log k) + (log N/B) - 2(log k) +… + 1 会有R次I/O,故读放大为R,即O((log N/B)*(log N/B)/(log k))
Size-tired LSM Tree
假设数据集大小为N,放大因子为k,最大层有k个大小为N/k个文件,倒数第二层有k个N/kk个文件…那么一共有O((log N/B)/(log k))层
写放大:同一个record,在每一层只会写一次,所以写放大等于层数,即O((log N/B)/(log k))
读放大:每一层读k个文件,一共O((log N/B)/(log k))层,故一共需要读O(k(log N/B)/(log k))个文件,不同于Leveld LSM Tree,一个文件不只是一个block B,而是有很多blocks,近似O(N/B)个,在文件内部二分查找找到对应的block需要O(log N/B),故整体需要O(k(log N/B)(log N/B)/(log k))次I/O,即读放大为O(k(log N/B)(log N/B)/(log k))
总结

- Fractal Tree Index 在写放大和读放大方便表现的都很不错
- Leveld LSM Tree 在写放大方面和FTI差不多,但是读放大方面比FTI要差
- Size-tired LSM Tree 在写放大方面优于FTI和Leveld LSM Tree,但读放大方面表现最差,一般少读多写并对写性能有较高要求的场景下考虑使用Size-tired LSM Tree
- B+ Tree 有较高的写放大,但是在读放大方面不错