How Many B+Tree Searches Are Hidden Inside a MySQL Insert？

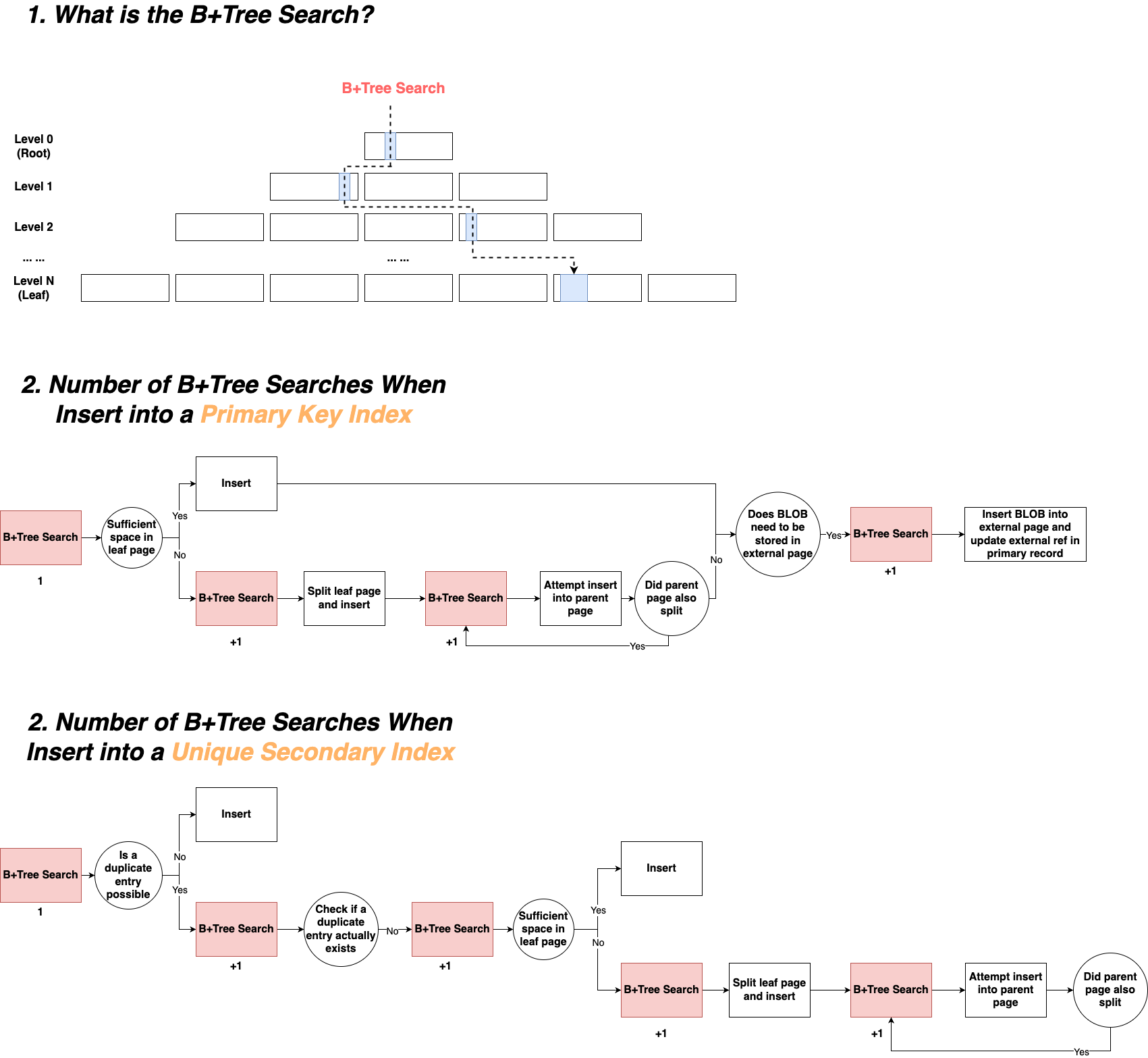
1️⃣ What is a B+Tree Search?

• A B+Tree search starts from the root page and traverses down level by level, comparing keys until the target page at the specified level is located. Typically, the target level is 0 (leaf level), but during page splits or merges, the parent level may also be involved.
• B+Tree search is a core operation in InnoDB’s B+Tree handling. The key function is ‘btr_cur_search_to_nth_level()’. Insert, update, delete, and read operations all require B+Tree searches.
• During a search, latches are acquired depending on the operation type. A read typically only latches the leaf page (S latch). For writes, optimistic inserts latch the leaf page (X latch), while pessimistic inserts may X latch the entire subtree involved in a page split or merge.
• The cost of a B+Tree search includes potential page reads from disk, page latching and index locking, and key comparisons at each level.

2️⃣ Number of B+Tree Searches When Inserting into a Primary Key Index

• 1st search: Locate the leaf page where the new record should be inserted. If there’s enough space, insert directly. Otherwise:
• 2nd search: Latch the subtree involved and split the leaf page, then insert.
• 3rd search: Locate the parent page of the split leaf and insert a pointer to the new page. If the parent page has enough space, insert directly. Otherwise, split the parent page:
• Extra searches: If the parent page also needs to split, recursively search and update higher-level parent pages, up to the root. This could require up to (B+Tree height - 2) additional searches.
• 4th search: If the record contains large BLOB fields stored externally, locate the newly inserted record again to insert the external BLOB, and update the external reference.

➔ Maximum number of B+Tree searches: 5 + (B+Tree height - 2)

3️⃣ Number of B+Tree Searches When Inserting into a Unique Secondary Index

• 1st search: Locate the leaf page to find the appropriate insertion position and check for potential duplicate keys. If potential duplicates are found:
• 2nd search: Locate the first candidate and perform a rightward lock scan (Next-Key Locking) to check for delete-marked records. If a non-deleted duplicate is found, return a duplicate key error. Otherwise, continue scanning to the right until encountering the first non-matching record, at which point the scan stops.
• 3rd search: Re-locate the correct position to insert after ensuring no duplicates. If the leaf page lacks space:
• 4th search: Latch the subtree and split the page.
• 5th search: Locate the parent page to insert a new pointer for the split page. If the parent page is full, recursively split:
• Extra searches: As with the primary key, this may cascade upward, requiring up to (B+Tree height - 2) additional searches.

➔ Maximum number of B+Tree searches: 6 + (B+Tree height - 2)

💡Additional Note on the 2nd Search for Unique Secondary Index Insertions

Some might wonder: why is a second search necessary to check for duplicates? Why can’t we verify duplicates directly during the first search?

The reason is that, unlike the primary key index, secondary indexes in InnoDB do not perform in-place updates. Instead, updates are handled by marking the old record as deleted (delete mark) and inserting a new record. As a result, even for a unique secondary index, there may be multiple records internally with the same indexed column values. The position where the first search stops might not point to a valid, active duplicate entry — it could be a delete-marked record — while the real active record might be located elsewhere. Therefore, a second search is needed, starting from the leftmost potential duplicate, to scan and validate whether a true duplicate exists.

💡A Potential Optimization Idea I Can Think Of:

If the first search already stops at a valid (non-delete-marked) duplicate entry, it might be possible to directly acquire the necessary locks and return a duplicate key error, without requiring a second full search. This could potentially reduce some overhead in certain cases.