【Paper笔记】The Log structured Merge-Tree（LSM-Tree）

Leveldb和Rocksdb的代码看了不少，对LSM-Tree的实践应该算是比较了解了，之前对LSM-Tree的理解也是站在实践的角度有一个感性的认识，最近读了下96年的原论文，从理论出发进一步理解一下LSM-Tree。写篇博客用整理下学习到的内容吧。

一. 为什么要有LSM-Tree

文章上来就举一个写多读少的例子，对于大量写入操作的场景下，B-Tree的写入会带来额外的I/O开销

Unfortunately, standard disk-based index structures such as the B-tree will effectively double the I/O cost of the transaction to maintain an index such as this in real time, increasing the total system cost up to fifty percent.

所以需要引入一种新的algorithm来应对这种场景，所以LSM-Tree应运而生

The Log-Structured Merge-tree (LSM-tree) is a disk-based data structure designed to provide low-cost indexing for a file experiencing a high rate of record inserts (and deletes) over an extended period.

LSM-Tree的核心思想就是将写入推迟(Defer)并转换为批量(Batch)写，首先将大量写入缓存在内存，当积攒到一定程度后，将他们批量写入文件中，这要一次I/O可以进行多条数据的写入，充分利用每一次I/O。

当然文章也如实提出，LSM-Tree在读取时会有短板

However, indexed finds requiring immediate response will lose I/O efficiency in some cases, so the LSM-tree is most useful in applications where index inserts are more common than finds that retrieve the entries.

二. The Five Minute Rule

文章有提到这个，很有意思的理论，所以找了下1985年原论文读了下

Pages reference every five minutes shoule be memory resident

文章结论就是如果磁盘某一页上的数据访问频率大于5分钟1次，那么就应该将这个页缓存在内存中。

证明如下：

  1. 一块容量180M，IOPS为15，价值$15k的磁盘，1秒1次(per access per second )IO的价值是（$15k / 15) 是 $1k/a/s，再算上这次I/O额外的CPU开销差不多$1k/a/s，那么1秒1次的I/O价值为$2k/a/s
  2. 一块容量1M，价值为$5k的内存，那么1KByte就是$5

1KByte的数据，在1a/s时，如果缓存在内存，也就是用内存$5的开销来换取磁盘$2k的开销，那么还是非常划算的，在0.1a/s时，是$5换$200，同样划算，继续提高访问频率，差不多到(2000 / 5)a/s时持平，也就是也就是400s访问一次，差不多5分钟

后来看(wikiedia)[https://en.wikipedia.org/wiki/Five-minute_rule]有计算公式，我结合论文整理一下吧：

设：

​ RI: 两次访问同一页的间隔秒数（expected interval in seconds between reference to the page）

​ M$: 一个字节内存的价值（be the cost of a byte of main memory ($ / byte)）

​ A$: 一次I/O的价值（be the cost of a disk access per second ($ / a / s)）

​ B: 一条数据的大小（the size of the record/data to be stored in bytes）

​ Bmax: 磁盘单次IO最大的数据大小（be the maximum transfer size of the disk in bytes）

假设：

​ B < Bmax

则：

​ A$ / RI = M$ * B

​ RI = A$ / (M$ * B)

​ A$ = PricePerDiskDrive / AccessPerSecondPerDisk

​ M$ * B = PricePerMBofRAM / PagesPerMBofRAM

所以：

​ RI = (PricePerDiskDrive / AccessPerSecondPerDisk) * (PagesPerMBofRAM / PricePerMBofRAM)

The Five Minute Rule给了我们一个简单认识，当程序占用的磁盘io越来越多的时候，需要适时考虑引入内存来合理的规划总开销。

3. LSM-Tree结构

以two-component为例，首先内存中有一个C0，它可以是AVL等结构，所有写入首先写到C0中。然后磁盘上有一个类B-Tree的C1，初始时为空，当内存C0的大小大到一定程度的时候，就需要进行rolling merge，它将其内的部分内容dump到C1中，它会将其数据从左到右（从小到大），一次追加写到C1的一个multi-page block页节点buffer中，如果这个叶节点buffer满了，就将其写入到磁盘，以此类推，直到C0扫描到最右（最大），此时C1首次生成。

之后如果C0又满了，后续的rolling merge就需要建立C0和C1的类似Merge Iterator的迭代器，顺序迭代数据到C1新的叶节点的buffer中（满了会写入磁盘），直到C0大小恢复到阈值之下，然后下次再满了，就接着上次Merge的位置接着向下迭代Merge，直到C0继续到大最右，在将C0和C1重新从最左开始建立新的Merge Iterator

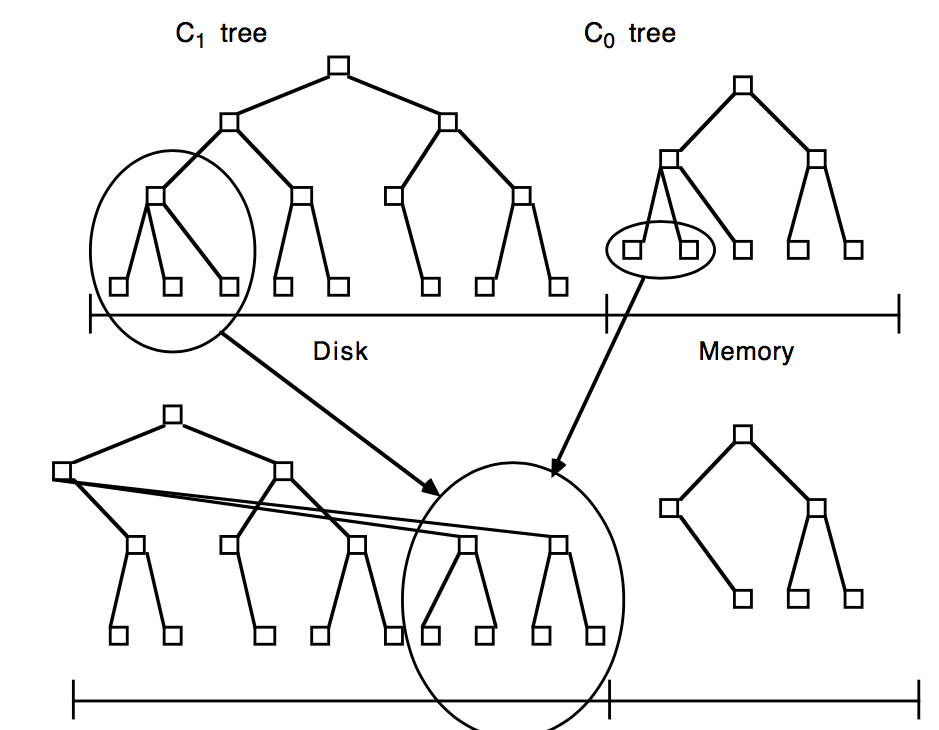
在大量写入场景下LSM-Tree之所以比B-Tree要好，得益于一下2个原因：

  1. multi-page block：不同于B-Tree，LSM-Tree的延时写(数据可以积攒)可以有效的利用multi-page block，在Rolling Merge的过程中，一次从C1中读出多个连续pages，与C0进行Merge，然后一次向C1写回这些连续pages，这样有效利用单次I/O完成多个pages的读写（B-Tree在此场景下无法利用multi-page的优势）
  2. batch：同样因为延迟写，LSM-Tree可以在Rolling Merge中，通过一次I/O批量向C1写入C0多条数据，那么这多条数据就均摊了这一次I/O，减少磁盘的I/O开销

无论怎样，尽可能减少数据写入的I/O开销，这也就是LSM-Tree的核心竞争力

4. The Disk Model

有了上节提到的multi-page block，我们就需要计算它带来的实际收益，首先定义两个概念，I/O Cost和Data Temperature。

1. I/O Cost:

​ 我们花钱买的磁盘，主要是给两个东西付费，1是容量，2是I/O。当我们在向磁盘写入数据的时候，而且其一会成为瓶颈：

1. 假如容量成为瓶颈，此时数据量巨大，以B+ Tree为例，层级会比较高，每次insert都要经过层层中间节点才可以找到叶节点进行写入，对应用来说，I/O的有效利用率不会很高（大部分都在读取中间节点） 2. 假如I/O成为瓶颈，也就是说I/O的有效利用率非常高，此时以上为例，B+ Tree的层数很低（这样大部分I/O是消耗给了叶节点），这就说明磁盘空间占用不会很高。

更通俗的说，如果磁盘保存的数据基本没有访问，那么我们对磁盘的开销就支持容量开销，随着访问频率的逐渐增加，开销会渐渐从容量开销主导转为I/O开销主导

现在就来推导一下整体开销的计算公式：

设：

​ COSTd: 1MByte磁盘的价值开销（cost of 1 MByte of disk storage）

​ COSTm: 1MByte内存的价值开销（cost of 1 MByte of memory storage）

​ COSTp: 1秒1次随机访问某个page的I/O开销（disk arm cost to provide 1 page/second I/O rate, for random pages）

​ COSTπ: 1秒1次访问某个multi-page block的I/O开销（disk arm cost to provide 1 page/second I/O rate, as part of multi-page block I/O）

场景：

​ 数据总量S MBytes，以1秒1次的频率访问H个pages（reference a body of data with S MBytes of storage and H random pages per second of I/O transfer(assuming no data is buffered)）

则：

​ H * COSTp: 磁头开销（rent for disk arms）

​ S * COSTd: 容量开销（rent for disk medium）

当H很小的时候，开销主要花在容量上，即S*COSTd，随着H的增长，磁头开销越来越大，即H*COSTp磁盘开销所以磁盘开销COST-D为：

​ COST-D = max(S * COSTd, H * COSTp)

H继续增长，长到Five Minute Rule的频率范围内，此时就在内存中缓存部分数据各位合适，所以此时的磁盘开销COST-B为：

​ COST-B = S * COSTm + S * COSTd

所以，统一的，磁盘最开销COST-TOT为：

​ COST-TOT = min(max(S * COSTd, H * COSTp), S * COSTm + S * COSTd)

如上所述，COST-TOT是随着H/S的增长而逐渐变化的

2. Data Temperature

基于上述H/S的比值变化，可以给出两个拐点：

  1. Tf = COSTd / COSTp 冰点（temperature divsion point between cold and warm data (“freezing”)
  2. Tb = COSTm/COSTp 沸点 （temperature divsion point between warn and hot data(“boiling”)）

Tf和Tb分别是上述COST-TOT公式中3个表达式切换的拐点，Tf是从S * COSTd向H * COSTp的拐点，Tb是从H * COSTp向S * COSTm + S * COSTd的拐点（由于COSTm » COSTd，所以在求比值的时候忽略S * COSTd，Tb的值有此而来）

下图给出了随着H/S变化，COST-TOT的变化图

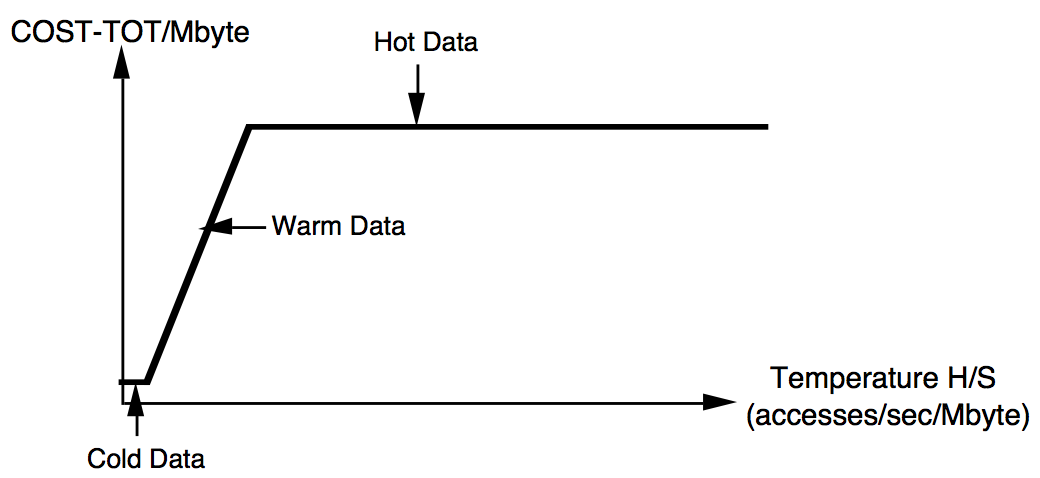
给出上面两个概念后，我们再来详细看一下multi-page block带来的好处，论文引用1989年IBM发表的测试报告得出结论：

COSTπ / COSTp ≈ 1 / 10

原文如下：

A 1989 IBM publiction analyzing DB2 utility performance on IBM 3380 disk:

… The time to complete a [read of a single page] could be estimated to be about 20 ms (assumes 10ms seek, 8.3ms rotational delay, 1.7ms read)… The time to perform a se- quential prefetch read [of 64 contiguous pages] could be estimated to be about 125ms (assumes 10ms seek, 8.3ms rotational delay, 106.9ms read of 64 records [pages]), or about 2 ms per page.

On SCSI-2:

SCSI-2 disk read of a 4 KByte page gives us a 9 ms seek, 5.5 ms rotational delay, and 1.2 ms read, totalling 16 ms. Reading 64 contiguous 4 KByte pages requires a 9 ms seek, 5.5 ms rotational delay, and 80 ms read for 64 pages, or a total of 95 ms, about 1.5 ms/page.

现在，我们给出一个具体例子，说明multi-pages block的好处：

环境：

​ SCSI-1:

​ Capacity: 1GByte

​ IOPS: 40

​ Disk Price: $1000

得到：

​ COSTm = $100/MByte

​ COSTd = $1/MByte

​ COSTp = Disk Price / IOPS = $25/(IOs/sec)

​ COSTπ = COSTp / 10 = $2.5/(IOs/sec) (The multi-block I/O advantage is significant)

由此算出：

​ Tf = COSTd / COSTp = 0.04 IOs/(sec * MByte) (冰点、”freezing point”)

​ Tb = COSTm / COSTp = 4 IOs/(sec * MByte) (沸点、”boiling point”)

如果将Tf和Tb计算公式的COSTp换成其1 / 10的COSTπ，可以看到其冰、沸点都变高，收益可观（尽可能的将上图中的冰点及沸点向右移）

继续往下使用Tb应用一下Five Minute Rule，算出其合理RI：

​ (1 / RI) * COSTp = pagesize * COSTm

​ pagesize = 0.04MByte

​ RI = (1 / pagesize) * (COSTp / COSTm) = 1 / (pagesize * Tb) = 62.5 second/IO

5. 与B-Tree的开销比较

1. B-Tree insert cost formula

首先，需要假设前提：

successive inserts to the tree are to random positions at the leaf level, so that node pages in the path of access will not be consistently buffer resident because of past inserts

即insert是随机的，这样索引至各个叶节点的缓存数据不会持续特别久，如果insert的数据是顺序的，即在下部叶节点是从左到右写的，那么索引节点的缓存可以完全hold住这样的场景，B-Tree在此场景下的性能也会很好。

在算B-Tree的insert开销前，我们先定义De（有效深度，effective depth）:

De, the average number of pages not found in buffer during a random key-value search down the directory levels of a B-tree

即在随机查找key-value时，从根节点到页节点路径上，page不在缓存的平均个数，它也就是每次访问叶节点数据的平均I/O次数

由于B-Tree的每次insert，一定是先找到对应叶节点（De次I/O），然后再将其写回去（1次I/O），所以B-Tree的insert开销是：

​ COSTb-ins = COSTp * (De + 1)

2. LSM-Tree insert cost formula

为了量化multiple-entities-per-leaf batch effect，我们定义首先M：

M for a given LSM-tree as the average number of entries in the C0 tree inserted into each single page leaf node of the C1 tree during the rolling merge

即M是在rolling merge过程中，C0 merge到 C1的一个page leaf node的平均entry个数，见下图

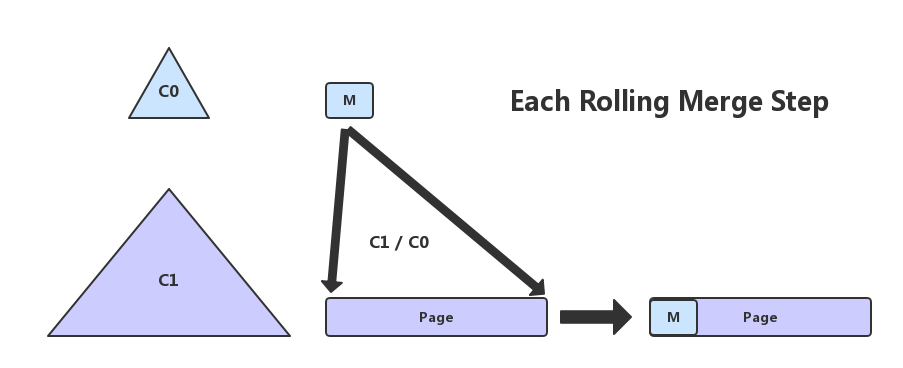
继续给出其他定义：

​ Se = （entry的size字节大小）entry size in bytes

​ Sp = （page的size字节大小）page size in bytes

​ S0 = （C0中所有叶节点的size大小）size in MBytes of C0 component leaf level

​ S1 = (C1中所有叶节点的size大小) size in MBytes of C1 component leaf level 则：

​ Sp / Se = （一个page中entry的个数）the number of entities to a page

由以上定义得到M的计算公式

​ M = (Sp / Se) * (S0 / (S0 + S1))

解释一下，(Sp / Se) 是每个page中的entry个数，那这么多个entry中，有多少个是从C0中Merge下来的呢，有

S0 / (S0 + S1)个，所以二者的乘积便是M的值。

有了以上定义之后，LSM-Tree的insert开销也便可以给出，数据的真正写入是发生在rolling merge时，那么一次rolling merge的有效写入数据其实就是从C0中Merge得到的，一次rolling merge的开销是对C1的叶节点的一读一写两次I/O，不过这里是上面所说的multi-page block，所以2次开销为2 * COSTπ，这两次开销实际是为了写入M个有效数据，所以M条数据均摊了这些开销，那么平均一条的写入开销为：

​ COSTlsm-ins = 2 * COSTπ / M

3. 对比

将COSTlsm-ins和COSTb-ins作比：

​ COSTlsm-ins / COSTb-ins = K1 * (COSTπ / COSTp) * (1 / M)

其中K1 = 2 / (De + 1)，它接近一个常量，这么一来二者的比值就取决于

  1. COSTπ / COSTp
  2. 1 / M

有没有很熟悉，这不就是我们第3节说到的LSM-Tree相比于B-Tree进行insert时的两个优势吗？

1. COSTπ / COSTp：multi-pages block
2. 1 / M：batch

当B-Tree在进行大量随机写入时，换成LSM-Tree可以有效减少磁盘I\O开销。

6. Multi-Component LSM-Trees

在上一节的COSTlms-ins / COSTb-ins中，如果M < K1 * (COSTπ / COSTp)，二者的比值便会大于1，导致LSM-Tree的反而性能不如B-Tree，原文是这样说的：

when M < K1 * (COSTπ / COSTp), this could even cancel the batching effect of multi-page disk reads, so we would do better to use a normal B-tree for inserts in place of an LSM-tree

所以在实际情况中，M的大小至关重要，而M的大小又和C0及C0 / C1的值息息相关，那么C0取多大就比较关键。

首先假设这么一种情况：

一个Two-Component LSM-Tree，有每秒R字节的数据持续写入C0

用户每秒R字节的写入速度要求rolling merge也得以恒定速度将数据Merge到C1才能保持C0的大小在其阈值范围内，此时C0的不同大小会有不同的结果：

  1. C0非常小：此时一条数据的insert都会使得C0变满，从而触发rolling merge，最坏的情况下，C0的每一次 insert都会导致C1的全部叶节点被读出来又写回去，I\O开销非常高
  2. C0非常大：此时C1基本没有I\O开销，但内存开销巨大

由此来看C0不宜取两端极值，所以我们假设从C0非常大开始，逐渐减少它的大小，来找最平衡的点：

  1. C0非常大：同上分析
  2. 减少C0大小：此时会有数据rolling merge到C1，使用部分inexpensive的磁盘空间来换取expensive的内存
  3. 继续减小C0：直到C1的I/O开销增长到最大（a point where the disk arms sitting over the C1 component media are running at full rate）

此时对于Two-Component的开销平衡已基本到头，有没有什么办法进一步减小呢？有，那就是在C0和C1之间引入一组新的Component，大小介于2者之间，逐级增长，这样C0就不用每次和C1进行rolling merge，而是先和中间Component进行，当中间Component到达其大小限制后在和C1做rolling merge，这样就不是C0就不用直接对阵C1，所以M不会特别小，从而可以在减少C0大小（内存开销）的同时减少磁盘I\O开销

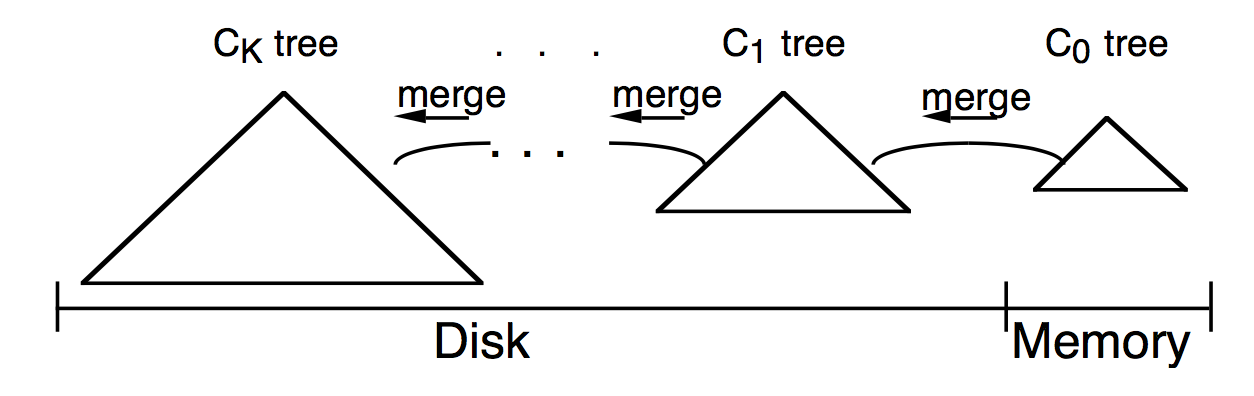
Component Size

对于Multi-Component而言，我们定义Si为第i级Component的大小，那么对于K+1 Component而言，总的大小S即为:

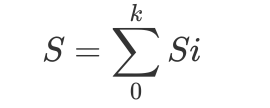\(S = \sum\limits_{0}^{k} Si\)

我们假设：

1. 用户以每秒R字节的写入速度往C0插入数据
2. 除Ck外，其余每一级Component都已经达到它的Threshold
3. Ck的大小相对稳定

另外，定义ri为相邻两级Component的size threshold比例，即:

​ ri = Si / Si-1

给出定理：

Given an LSM-tree of k+1 components, with a fixed largest-component size Sk, insert rate R, and memory component size S0, the total page I/O rate H to perform all merges is minimized when the ratios ri = Si/Si-1 are all equal to a common value r.

即当r1 = r2 = … = rk = r时，各级Component进行merge带来的总的磁盘I\O，即H会最小，此时有

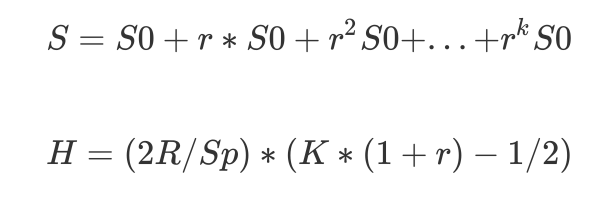\(S = S0 + r*S0 + r^{2}S0 + ... + r^{k}S0\)

\[H = (2R/Sp) * (K * (1+r)-1/2)\]

其中Sp是一个page的字节大小。

证明定理:

C0以R Bytes/s的速度写入，就要求各级Component Ci-1以同样的速度R merge到Ci，每次merge，对于Ci-1，会每秒读出R/Sp个pages（multi-pages block），然后Ci每秒读出ri * R / Sp个pages，进行merge，最后向Ci每秒写入(ri + 1) * R /Sp个pages，如此一来，总的I\O开销H为：

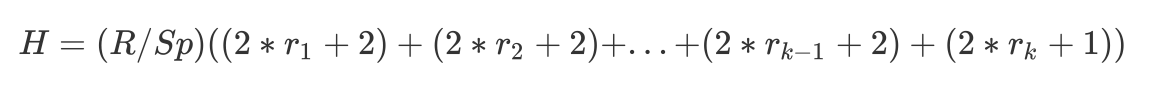\(H = (R / Sp) ((2*r_{1}+2)+(2*r_{2}+2)+...+(2*r_{k-1}+2)+(2*r_{k}+1))\)

即：

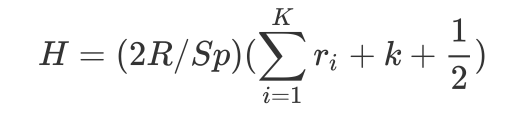\(H = (2R/Sp)(\sum\limits_{i=1}^{K}r_{i} + k + \frac{1}{2})\)

因为有：

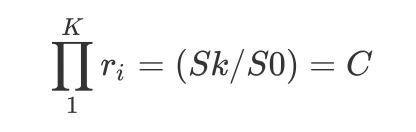\(\prod\limits_{1}^{K}r_{i} = (Sk / S0) = C\)

所以我们可以将

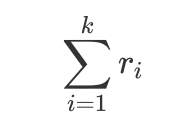\(\sum\limits_{i=1}^{k}r_{i}\)

表示为：

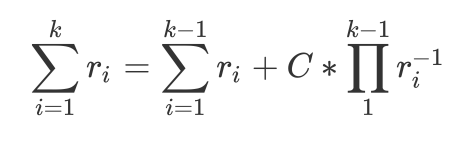\(\sum\limits_{i=1}^{k}r_{i} = \sum\limits_{i=1}^{k-1}r_{i} + C*\prod\limits_{1}^{k-1}r_{i}^{-1}\)

我们对每一个ri求偏导数，令其为0，即

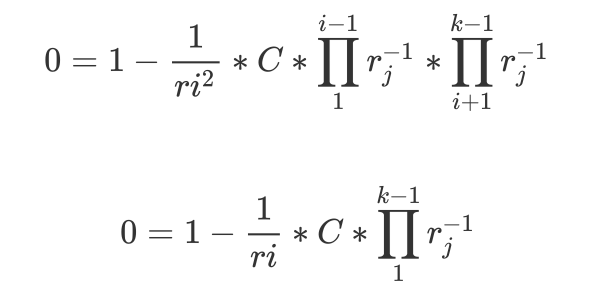\(0 = 1- \frac{1}{ri^2}*C*\prod\limits_{1}^{i-1}r_{j}^{-1}*\prod\limits_{i+1}^{k-1}r_{j}^{-1}\)

\[0 = 1- \frac{1}{ri}*C*\prod\limits_{1}^{k-1}r_{j}^{-1}\]

所以当每一个ri同时为

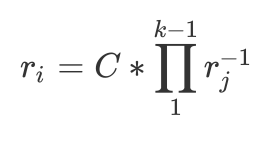\(r_{i} = C*\prod\limits_{1}^{k-1}r_{j}^{-1}\)

其偏导数为0，H取的最小值

Minimizing Total Cost

对于Two-Component，其总I\O开销COSTtot为：

​ COSTtot = COSTm * S0 + max[COSTd * S1, COSTπ * H]

令：

​ s = (COSTm·S0)/(COSTd·S1) = S0内存开销与S1数据的存储开销之比

​ t = 2·((R/Sp)/S1)·(COSTπ/COSTd)·(COSTm/COSTd)

那么总开销COSTtot与S1的数据存储开销之比：

​ C = COSTtot / (COSTd * S1)

代入COSTtot：

​ C = (COSTm·S0+max[COSTd·S1，COSTπ·H])/( COSTd·S1)

C = (COSTm·S0) /( COSTd·S1)+max[1, COSTπ·H/( COSTd·S1)]

因为是Two-Component，所以H=2(R/Sp)(r+1/2)，代入：

​ C = s+max[1,2((R/Sp)/S1)( COSTπ/COSTd)(r+1/2)]

​ C = s+max[1,2((R/Sp)/S1)( COSTπ/COSTd)(COSTm/COSTd)(COSTd/COSTm)(r+1/2)]

​ C = s+max[1,t(COSTd/COSTm)(r+1/2)

又因为r = S1/S0，所以：

​ C ≈ s+max[1,t(COSTd/COSTm)(S1/S0)

​ C ≈ s+max[1,t(COSTd·S1)/(COSTm·S0)]

​ C ≈ s+max[1,t/s]

这也意味这在C中(COSTπ * H) / (COSTd * S1) ≈ t/s

在t中，COSTπ/COSTd表示multi-pages block下的I\O开销与容量开销的比值，接近常量，COSTm/COSTd表示内存开销与容量开销的比值，也接近常量，(R/Sp)/S1表示每秒写入R数据对应的page在S1的占比，类似数据密度，可以看出来t与R成正比

我们假设t/s=1，即(COSTπ * H) / (COSTd * S1) = 1，说明此时磁盘I\O和容量平衡，以此为界：

​ 当t<1时，C在t = s时取的最小值

​ 当t>1是，C在s=t^(1/2)时取的最小值2*t^(1/2)，此时将C代入C = COSTtot / (COSTd * S1)，得到：

​ min(COSTtot) = 2[(COSTm·S1)(2·COST·R/Sp)]^(1/2)

因此在t>=1的情况下，LSM-tree的总开销看起来是(足以将所有LSM数据保存下来的所需内存的开销，这是一个很高的值，即COSTm·S1)和(用于支持将插入数据写入到磁盘所需的multi-page block IO的磁盘开销，这是一个很低的值，即2·COST·R/Sp)之乘积的几何平均数的2倍。总开销中的一半将会被用于S0的内存开销，剩下的一半用于对于S1的IO访问开销。磁盘存储空间的开销并没有体现出来，因为t>=1保证了数据是足够热的足以让IO开销占据磁盘开销的主导。

在t<=1的情况下，数据较冷的情况下，在s=t时可取得最小化开销，此时C=t+1<2。这意味着这种情况下的总开销总是不会超过用于将S1存储在磁盘上的开销的两倍。在这种情况下，我们会根据存储开销来决定磁盘大小，然后通过利用起它所有的IO能力来最小化内存使用。

7. 总结

multi-pages block和batch两大杀器成就了LSM-Tree在大量随机insert时的高性能，以后有时间还得把这篇论文翻出来读一读，也许会有更深的体会。